Das Muster
Bild Siebert: BiXnom-PLUS (2)
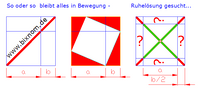
Diese Webseite zeigt einen Würfelbausatz, der zu dekorativen Zwecken ein selbst zu flechtendes Muster enthält. Das Zahlenelement ist die Diagonale einer Teilfläche. Die Zahlen 1 - 6 eines Spielwürfels sind die Summe der Elemente einer Würfelseite, d.h. wachsende Strichlänge statt üblicher Punktmenge. Der BiXnom drittelt seine Kanten: c = b/2 + a + b/2. Kein Trinom, sondern Binom durch Zellteilung. Von 9 symmetrischen Teilflächen einer Seite werden 5 von 2 Diagonalen durchkreuzt. Die diagonale Strichlänge symbolisiert 6 Zahlen: 1 = / ; 2 = x ; 3 =... ; 4 =... ; 5 = ... ; 6 = X . Diagonalstriche bilden Dreiecke, damit Vierecke nicht umfallen. Somit ist die Seite 6 (X) stabil, aber die übrigen Seiten haben statische Defizite. Auf der Seite 6 (X) verbleiben dennoch 4 nicht durchkreuzbare Vierecke von eigener Qualität. Zu deren NICHTS weiß die Mathematik nichts – hier sei es das UNBERECHENBARE.
Bild Siebert: BiXnom-Würfelzahlen
Der BiXnom bildet auf der Seite der Zahl 1 (/) mit einem Minus die 2. Binomische Formel und auf der gegenüberliegende Seite der Zahl 2 (x) mit einem Plus die 1. Binomische Formel ab. Die Summe dieser Seiten ist 3, womit es kein üblicher Spielwürfel mit Summe 7 ist. Er zeigt die altertümliche Zahlenanordnung des quaderförmigen Wikinger-Würfels, der die 1 und 2 an seinen Enden trägt, womit diese schwerer zu werfen waren.
Der BiXnom zeigt auf den 4 nicht durchkreuzbaren Teilflächen der Seite 1 (/) ein Minus (-) und auf der Seite 2 (x) ein Plus (+). Zahl und Vorzeichen sind in der Form ähnlich. Die Vorzeichenflächen sind nicht durch Diagonalen stabilisiert und bringen daher Veränderungen zum Ausdruck. Sind 2 Würfel im Spiel, kann ein Strom von Plus nach Minus für eine Spielrichtung gelesen werden - dies erzeugt mehr Funktionalität.
Der BiXnom bringt seine 6 Seiten in einen räumlichen Zusammenhang: Die Vorzeichen der Würfelseiten 1 (/) und 2 (x) gelten um die Kante herum auch für die Seiten 3, 4, 5 und 6, die außerdem ein Netzmuster zeigen. Weil sich die Seiten 1 und 2 gegenüberliegen, stehen Plus- und Minus-Kanten nicht über Eck. Die 3. Binomische Formel auf den Seiten 3, 4, 5 und 6 muss daher so gelesen werden, dass sie am HALBSTEIN jeweils zur Hälfte abgebildet wird. An der Stoßkante stehen halbe Vorzeichenflächen mit gegensätzlichen Vorzeichen aneinander. Sie neutralisieren sich und werden im Muster nicht mit angezeigt. Die Wirkung „Zwei Seiten einer Medaille“ wird hierdurch verstärkt. Um die Zahlenwerte des Musters teilweise mit einer Flechtschnur darzustellen, ist die Konstruktion mehrteilig. Erst die Kreuznaht als vertraute Handarbeit fängt Blicke ein: Das kann ich auch! Wirkt wie Rauch im Bienenstock. Vom sattsam Erwähnten nun fix zum Register „Der Bausatz“ wechseln.
Im BiXnom ist intuitiv zu sehen, wo man Brücken bauen muss, damit alle Teilflächen einer Seite in relative Ruhe kommen. Aha-Erlebnis! ["Die Mutter aller Tische", gefunden 2018 in der Arminius-Markthalle in Moabit, ist allerdings eine lange Rittertafel für eine Busladung voller Gäste. http://www.markthalleberlin.com/de/eat-and-drink/hofladen/ ]
Daraus kann die Idee entspringen, sich dem UNBERECHENBAREN neugierig zu nähern.
Das UNBERECHENBARE ist bei Strömungen aller Art negativ, weil die Theorie mehr ergibt, als es wegen der Reibungsverluste praktisch möglich ist. Folglich wird die Theorie durch einen Schummelfaktor kleiner 1 angepasst. Der umgekehrte Fall ergibt einen positiven Wert: Passen in den Schwimmring mehr hinein, als man es sich hätte vorstellen können, dann muss die Theorie mit einem Sicherheitsfaktor größer 1 angepasst werden, falls der Steg zu schmal wird.
Wird die Möglichkeit zum Experiment nicht geboten, ist der Nachlass vieler Forschergenerationen hilfreich, dem UNBERECHENBAREN auf die Spur kommen. Aus dem Würfel heraus wäre es eher sportlich zu sehen, Erfolg ist aber bei jedem Thema möglich. Zunächst aufwärmen!
Die 2 in der binomischen Formel wird von der Natur gern angenommen. Natur macht nicht die 2 Sicherheitsnachweise des Ingenieurs gegen das Gleiten und Kippen eines Baukörpers, sondern hat den Sicherheitsfaktor 2 in nur 1 Nachweis. Im ungünstigsten Fall ist das gerade ausreichend. [Aber der risikoscheue Ingenieur schreibt auch die Sicherheit 2 vor, und zwar für Heizöllagertanks aus Kunststoff. Zitat Bundesverband Lagerbehälter e.V., 2015: „Diese „doppelte Sicherheit“ sollte man nicht ausreizen, deshalb empfehlen wir ....zu ersetzen.“]
Zur Erforschung ist es günstig, wenn jedes Ding aus 2 Teilen besteht, dem Bekannten und dem UNBERECHENBAREN. Beide Teile haben die gleiche Geschwindigkeit, z.B. beim Redefluss mit dem Gesprächspartner vis-a-vis. Immer wechselseitig ist der Andere der UNBERECHENBARE, sonst wüsste man schon vorher, was gleich gesagt wird. Viel reden und wenig sagen, beeindruckt den Gesprächspartner, insbesondere wenn es wegen der 2 noch wiederholt wird. Die gleiche Redegeschwindigkeit kürzt sich zur relativen Ruhe weg, aber das Binom (a+b) wird zum quadratischen, turbulenten Spielfeld (a+b)². Somit ist die Größe 2ab/(a+b)² der Maßstab für das UNBERECHENBARE...und das sieht man. Womit man es allerdings noch nicht berechnet hat.
So etwas Ähnliches kommt in der Quantenphysik als hohe Wissenschaft ganz fett heraus. Zitat aus Wikipedia: „Ausgangspunkt des Pauli-Prinzips ist die Tatsache, dass identische Teilchen in der Quantenmechanik unterscheidbar sind: Der Verlauf eines Experiments oder allgemein die Entwicklung eines physikalischen Systems kann sich nicht ändern, wenn man darin zwei identische Teilchen vertauscht. Quantentheoretisch ergeben sich aber bei Vertauschung identischer Teilchen nur dann die gleichen Messwerte, wenn das Betragsquadrat der (Gesamt-)Wellenfunktion gleich bleibt, sich also allenfalls der Phasenanteil der Wellenfunktion ändert. Die experimentelle Erfahrung hat sogar die weitergehende Tatsache gezeigt, dass bei Vertauschung zweier identischer Teilchen je nach Teilchenart die Wellenfunktion entweder unverändert bleibt oder nur ihr Vorzeichen wechselt.“
Dem Einfachen weiter auf der Spur... Die Geometrie der ZWEI
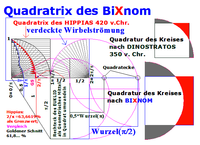
Die Flächengleichheit von Rechteck und Quadrat wird nach EUKLID über die Konstruktion des Geometrischen Mittels erzeugt (siehe hier zuvor). Wird zunächst ein Viertelkreis flächengleich in ein Rechteck „transformiert“, dann ist die sogenannte "Quadratur des Kreises" nach DINOSTRATOS gelungen, sofern die Zahl p getrickst dem Taschenrechner entnommen wird. Die Transformation gelingt mit der QUADRATRIX des HIPPIAS: Im Einheitsquadrat 1x1 wird eine „kinematische Kurve“ erzeugt, die die Grundlinie von 0 = 0/p nach 1= p/p bei 63,66...% = 2/p schneidet [Goldener Schnitt bei 61,8..%]. Dieser Wert wird über Dreiecksproportionen zur Bildung des Rechtecks genutzt. Die kinematische Kurve entsteht aus 2 gleichzeitigen Bewegungen: 1.) Ein Punkt läuft von oben nach unten als Umweg über einem Viertelkreis in gleichen Winkelabständen von Y mit 90° nach X mit 0°. Dieser wird hier als Potentialströmung vom Typ Steinschleuder oder Schallplatte verstanden. 2.) Ein 2. Punkt läuft die Y-Achse von 1 nach 0 herab als horizontale Zeilen mit gleich vielen Lücken wie aus der polaren Winkelfolge. Die jeweiligen Schnittpunkte von Zeile und Strahl bilden eine kinematische Kurve, die auf der x-Achse bei 2/p endet. Die 2. Bewegung ist keine Drehbewegung (Drehpunkt bei unendlich), sondern vergleichbar mit einer horizontalen Potentialströmung vom Typ des elektrischen Stroms bzw. einer laminaren (nicht turbulenten) Wasserströmung - Sickerwasser, das durch den Porenraum zwangsweise geradlinig geführt wird.
Statt 2er Strömungen von der linken Seite wird für die relative Ruhe eine gleich große Gegenströmung als Wirbelströmung vom Typ Strudel bzw. Badewannenabfluss auf der rechten Seite benötigt. Diese wird in der Quadratrix des BiXnom nunmehr derart behandelt, dass die 1. Bewegung 50% schneller verläuft, weil in einem separaten 2. Vorgang durch den Strudel Wasser abgelaufen ist. Wird dieser verdeckte Vorgang mit berücksichtigt, wurde kein Viertelkreis, sondern ein Halbkreis durchlaufen. Die kinematische Kurve des BiXnom© veranschaulicht dann auch die Einwirkung eines Strudels, d.h. die merkwürdige Kurve macht Sinn.
Zur Quadratur des Kreises muss die Kantenlänge „c“ aus der Fläche eines Viertelkreises (Dinostratos) bzw. eines Halbkreises (Bixnom) berechnet bzw. durch eine Konstruktion aus der Quadratrix nachgewiesen werden [siehe https://de.wikipedia.org/wiki/Quadratrix_des_Hippias].
Kantenlänge c (Dinostratos) = Wurzel (p*r²/4 bzw. a (Bixnom) = Wurzel (p*r²/2) ; mit r=1 folgt;
Kantenlänge c (Dinostratos) = Wurzel (p/4 ) bzw. a (BiXnom) = Wurzel (p/2) = 1,253314...
Somit ist ersichtlich, dass der Wert Wurzel (p/2) beim BiXnom von Bedeutung ist.
Das Rechteck ergibt sich aus dem geometrischen Mittel a*b= c². Der Wert a =p/2 von DINOSTRATOS gilt weiterhin, aber b verdoppelt sich auf b (BiXnom)= [(Wurzel (p/2))^2]* (2/p)=1.
Zur Quadratrix siehe auch unter: https://download.uni-mainz.de/mathematik/Algebraische%20Geometrie/Lehre/Sem-Ausgewaehlte-hoehere-Kurven-WS2016-17/Deimer%20Rike_Die%20Quadratrix_080217.pdf
„Quadratur des...“, darf man doch nicht sagen! Genau, deshalb auch kein Google, kein Amazon etc. im Lande. Die Fragestellung wurde neuzeitlich so verdreht, dass statt unendlich genauem Werkzeug immer noch Zirkel und Lineal auf dem Tisch liegen.
Fräulein Schön: "Ich sah aus wie ein eingetretener Schuhkarton, dann hat mich Egon schön rund gemacht!"
Naturmodell mit Kontakthülle: Coronavirus SARS-CoV-2
[https://de.wikipedia.org/wiki/SARS-CoV-2]
Im BiXnom-Kunstprojekt wird anstelle einer einfachen Flächengleichheit ein Fomänderungsprozess durch Bildung eines gemeinsamen Gitterpunktes von Kreis und Quadrat gebildet. Die Gittergeometrie ist durch die binomische Streckenteilung b/a beschrieben, die sich nach Wahl einer Formvariablen „Formfaktor f“ ändert. Deren Wertebereich ist eingeschränkt: Ein quadratisches Faltpapier mit dem symmetrischen BiXnom-Gitter kann nur bis zur Mitte bei a=b eingeklappt werden. Aus dem Verhältnis von b/a kann ein Winkel gebildet werden. Eine Bedeutung kann nur der Sinus (nicht der Tangens) erreichen, denn er zeigt, wie der Kreisradius zum gemeinsamen Gitterpunkt ausgerichtet ist. Die technische Maximalneigung beträgt 45° und damit b/a=0,707. 45° bedeutet, dass man nur so viel Reibung erzeugen kann, wie man selbst wiegt. Eingesetzt in die BiXnom-Formel ergibt dies eine Formfaktor-Grenze von f=0,73417. Unter f=0,63 sind dann ab 90° auch mathematisch keine Ergebnisse vorhanden. Die Erdoberfläche bildet den bodenmechanischen Halbraum und daher eine technische Grenze bereits bei 45° statt 90°.
In der Würfelseitenansicht kann ein Würfel flach zusammengedrückt werden, bis sich seine Grundfläche in der Draufsicht doppelt gestreckt hat. Der Würfel ist 2 Radieneinheiten breit und plattgemacht = 4*R = 4*1,2533...= 5.01326. Die vorgenannte Formfaktor-Grenze bildet den Plus-Bereich ab, um den sich der maximale Minusbereich auf 5.01326 - 0,73417 = 4,279086 kürzt. Bei f= 1,2533 ist eine Nullstelle vorhanden. Hier würde ein Aräometer (Senkwaage, Dichtespindel, Hydrometer) nach dem Archimedischen Prinzip vergleichsweise aus der Flüssigkeit gehoben und dann in Schräglage einen Winkel anzeigen, bis es umfällt. Im Toten Meer ist die Dichte nicht <1, sondern mit 1,240 kg/Liter erheblich groß. Hier wird der Schwimmer zur Dichtespindel und lässt den Bauch sonnen. Im Sprudelwasser wird der Schwimmer zum sinkenden Stein. Beim Falten lässt sich eine Fläche unbemerkt auf die Rückseite klappen. Dies ist bei der mathematischen Lösung nicht möglich: Eine reduzierte Fläche lässt sich nicht beseitigen, sondern zeigt sich schwer verständlich als Minus-Größe.
Der Faltprozess hat mit der physikalischen Dichte nichts zu tun. Die visuell ersichtliche Eingangsfrage der Würfelkunde ist aber derart zwingend, dass die Natur dafür einer mathematischen Lösung folgen muss. Die BiXnom-Formel zeigt den einfachsten Weg. Natürlich gilt sie nur Flüssigkeiten, aber selbst Steine stammen aus einer heißen Schmelze. Für höhere Dichten muss dann zeilenweise immer wieder ein neuer Würfel aufgestapelt werden. Die Dichte wird dimensionslos als Bezug zur Wasserdichte dargestellt. Formfaktor 2,65 bedeutet einen Granit (Quarz, Feldspat und Glimmer) mit der Dichte von 2,65 kg/Liter und einen Kontaktwinkel (Reibungswinkel) von ca. 31°. Das ergibt in der Praxis einen Sand; der Kies kann durch seine Grobstruktur noch die 40° erreichen. Dafür müsste die Formel zur Erdstoffbeschreibung im Porenraum noch archimedisch aufgerüstet werden. Der Formfaktor f zeichnet sich in der Geometrie als relative Druckhöhe an den Gleichgewichtszuständen Schwimmen, Schweben, Sinken und Verdichten ab.
Bild Siebert: Geometrie der BiXnom-Formel
Das Ziel ist der Weg in die Unterwelt. Dazu muss in Kunstpausen immer auf eine höhere Eingebung gehofft werden. Kunstpausen folgen hier als „Der BiXnom-Bausatz“ und „Die Spiele“.
Die Inspiration lag in der deutschen Zigarettenstadt für Studenten kostenlos in der Luft. Malocher hatten sie als „Karo“ in der Tasche, Weißkittel schafften die Karriere von „Juwel“ zu „F6“, Inoffizielle Mitarbeiter von „Salem“ zu „Club“, der Gemüsehändler paffte auf der Pferderennbahn den Luxus „Duett“ zu 6 M und für Glückliche lag „Ernte 23“ im West-Paket. 2020 endlich wieder Mangel-Shutdown mit Bückware, ´raus durften nur Reisekader und Oma inhalierte die Letzte O2-Zigarette im Hühnerstall bäuchlings (das ist Satire).
dat 04/2020